Elegant Ellipses
![]()
While researching how to draw rotated ovals I learned some interesting facts about ellipses and thought I’d share them with you:
- Ellipse Definition: There are many ways to say it, but essentially an ellipse is just a circle stretched along one axis. Think, “smushed penny on a train track” or if you want to get technical about it you could say, “an ellipse is formed by a locus of points in a plane such that the sum of the distances to two fixed points is a constant.” Which means…
- One way to draw an ellipse is to:
- Tie a length (i.e. 12 inches) of string into a loop.
- Poke 2 pushpins into a board a set distance (i.e. 5 inches) apart.
- Loop the string around the pushpins.
- Place a pencil inside the looped string and rotate it around the pushpins while keeping the string taut.
- Holding the string taut while rotating the pencil will constrain it in such a way that the 2 distances from each pushpin to the pencil will always add up to the same amount (i.e. 7 inches). Or in other words, “the sum of the distances from to two fixed points (pushpins) is a constant (7”) which of course meets the aforementioned definition of an ellipse.
- Another way to make an ellipse: Take a cone (a round funnel), fill it with a liquid (beer) and tilt the funnel slightly being sure not to spill any of the precious liquid. Now look at the surface of the liquid. See how it makes that ‘ovally’ type shape? That’s an ellipse. It’s sort of interesting in a “roundish but not quite” kind of way. It has quadrilateral symmetry no matter how you tilt it which may seem a bit counter-intuitive. It seems odd that the side of the oval by the small round hole in the bottom of the funnel is the same size and shape as the side of the oval near the big round hole at the top of the funnel. Try it to see for yourself or try it as an excuse to drink some beer.
- Ellipse Terminology:
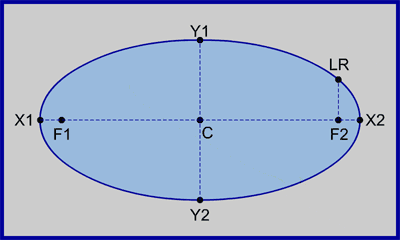
- Center = the point at C.
- Focus = the point at F1 or the point at F2.
- Foci = both points F1 and F2
- Major Axis = line X1—X2.
- Minor Axis = line Y1—Y2.
- Major Radius (also called Semimajor Axis) = line C—X2.
- Minor Radius (also called Semiminor Axis) = line C—Y2.
- Latus Rectum = line F2—LR.
- Ellipse Tips
- Area:
A = Math.PI * majorRadius * minorRadius;
- Distance from center to focus:
var majorR2 = majorRadius*majorRadius; var minorR2 = minorRadius*minorRadius; F = Math.sqrt(majorR2 - minorR2);
- Circumference (perimeter):
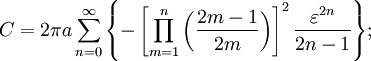
- Area:
- Ellipse Quips
- A 3 dimensional ellipse is called an ellipsoid.
- A circle is an ellipse where both foci overlap.
- Like a circle, determining the area of an ellipse is easy but unlike a circle, determining the circumference of an ellipse is difficult and requires calculus.
- All ellipses are ovals but not all ovals are ellipses. Anything egg-shaped is an oval but very few shapes are true ellipses.
- Elliptical rooms are good for eavesdropping because most of the sound generated at one focus is reflected directly back to the other point of focus across the room. Coincidentally, the president’s seat appears to be located at one focus of the Oval Office while visitors are seated near the other.
And that concludes our lesson on Ellipses for the day.
 RSS Feeds
RSS Feeds
awesome, thanks for the useful informations (especially the quips)
Delicious. Can’t wait to incorporate this into some scripted movement.